Dipole
Introduction
This study came about as a result of experimental computer simulations of Coulomb forces and interactions between protons and electrons in hydrogen atoms as well as between quarks in protons and neutrons. The simulations showed a weak but consistent and robust attraction between particles with zero external total charge irrespective of simulation parameters imposed on the particles. Also see older descriptions of London Dispersion Forces and Van der Waals Forces which are earlier known consequences of the same effect of mutual polarization of atoms and molecules.
Entanglement, strong force, gravity and magnetism are caused by subatomic attraction between charges and/or dipoles. As such it is part of quantum physics even if the underlying mechanism can be described in context of Coulomb forces in easy to understand classical physics shown below.
Entanglement
Action at a distance can be used to describe entanglement, gravity and magnetism. They are all the result of Coulomb forces between charged particles and/or dipoles. The main difference is the strength of the Coulomb link between them. While gravity and magnetism are caused by a Coulomb force between dipoles in neutral particles, entanglement is caused by the full Coulomb force between charged particles. Consequently the Coulomb force link between two entangled particles is 1/(9*10^-19) = 1.111*10^18 times stronger than gravity. Take for example the case of two electrons from the same atom and thereby entangled by having become synchronized. Even when separated by a long distance, observations suggest that if we disturb one to change for example its spin direction, so does the other one though it is seemingly undisturbed and far away except for its strong Coulomb force entanglement with its partner particle.
Strong force
Strong force holds neutrons and protons together to form the nuclei of elements.
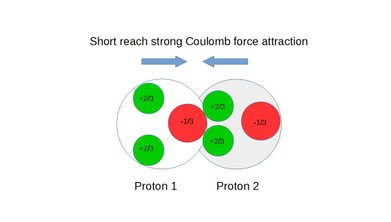
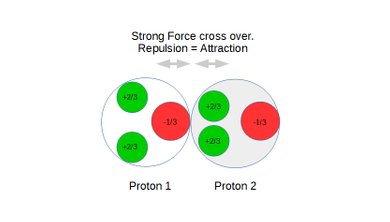
Strong force is the result of the nine competing Coulomb force vectors between the three quarks in each nucleon. These vectors are both attracting and repelling and the distance between respective pair of charges determine the strength of the individual force vectors which combine into a composite force.
At the minimum distance the composite force is attracting and called strong force. At a slight increase in distance between the nucleons the composite force becomes a repelling force associated with nuclear decay and often called weak force.
Gravity
Coulomb forces between atoms are both attracting and repelling. The separately computed individual forces are large but essentially cancel each other except for resulting in a weak, attracting compound force.
As a consequence of the mobility of charges and associated Coulomb forces, attracting charges pull together, slightly reducing their distance and increasing the force between them, while repelling charges push apart, slightly increasing their distance and reducing the force between them. Based on Coulomb's law the result becomes a slight advantage to the sum of attracting forces over the sum of repelling forces, such that the resulting force balance always yields a small, attracting net force between the atoms called gravity.
The polarization of atoms described above results in attraction and gravity between atoms and bodies with mass.
Magnetism
A permanent magnet is characterized by electron orbitals being parallell and unidirectional. This creates a magnetic north pole on one end and a south pole on the other end. Take two of these and place them end to end such that the orbitals are still unidirectional and you get the force of magnetic attraction between the two. Turn one around and you get a force of magnetic repulsion between the two.
Electromagnetism
Electromagnetism is the compound Coulomb force between currents of charge. Conductor coils replace the parallel ferromagnetic orbital planes with a coiled conductor carrying a current of electrons in parallel circular motions. Electromagnetic effects including the compound force between conductors A and B are complicated and best calculated by computer taking into account the geometry involved and forces between voltage A and charges in conductor B and vice versa.
Radiation
All charged particles are connected by electrostatic Coulomb force. This is undisputed and according to Cern this force propagates with the speed of c. When a charged particle or a group of particles is forced to oscillate, this oscillation is superimposed upon existing ES Coulomb radiation and transmitted to surrounding charged particles. Coulomb force radiations do not interfere under way. Instead the effect is determined by the recipient charge depending on the compounding of preexisting Coulomb forces and the frequency and force level of the additional Coulomb force(s) received. Examples are: Radio, wifi, microwave, light, and x-rays.
Gravitational lensing
Light is consequently propagated in form of an undulating Coulomb force which has the same effect on a body with mass as that caused by a mass with dipole Coulomb charge. This does not mean that light has what we call mass, only that it participates in dipole gravity and gravitational lensing as observed.
Third party conclusions
The conclusions above are consistent with the conclusions of a more recent quantum physics study from 1998 by Bernhard Haisch, Alfonso Rueda and H. E. Puthoff.
A NASA-funded research effort is also reported to be under way at the Lockheed Martin Advanced Technology Center in Palo Alto and at California State University in Long Beach.
Links to Hydrogen gravity simulations
The simulations presented below are performed in physically correct simulation software. The simulations shown use simple, electrically charged bodies to represent electrically charged particles using known mass and charge of the particles in question. The simulations do not attempt to reflect any nuclear interactions beyond Coulomb forces between particles and bodies. See details below.
Charge posturing, dipole formation and Coulomb attraction between 2 hydrogen atoms:
The moving red dot indicates the direction of the dipole axis from the proton to the center of charge of the electron orbital.
http://www.youtube.com/watch?v=QB-DYEmRo3o
https://www.youtube.com/watch?v=hFaL_ZFqQUI
https://www.youtube.com/watch?v=mS-KqlaiTf0
Mathematical evidence of unconditional net Coulomb attraction
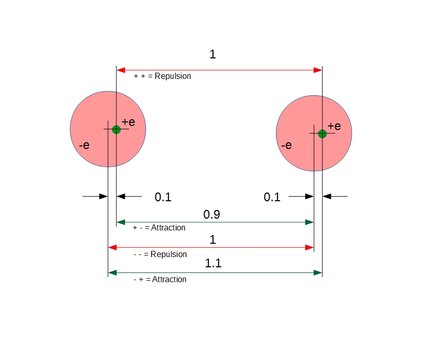
Figure 1. Conceptual example of conditional polarization according to Coulomb's law:
Attraction = ke* q^2* (/0.9^2 + e^2/1.1^2 - e^2/1^2 - e^2/1^2)
= ke* q^2* (1/0.81 + 1/1.21 - 1/1 - 1/1)
= ke* q^2* (1.23456790 + 0.82644628 - 1 - 1)
= ke* q^2* (0.06101418)
= ke* 0.061q^2
As can be seen in the result above, the Coulomb interaction between two atoms always yields a small, positive attracting force between the atoms.
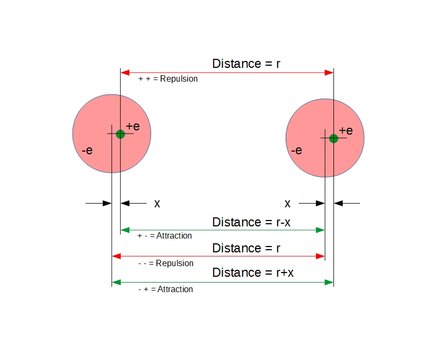
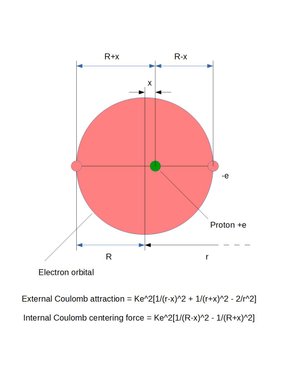
Calculation of dipole offset distance X between positive and negative charges in one of the atoms when 1*10^-10 meter apart above.
External:
K*e^2(1/(r-x)^2+1/(r+x)^2-2/r^2)
K=8.98755178787*10^9
e = 1.60217662*10^-19
r = 10^-10
Internal:
K*e^2(1/(R-x)^2-1/(R+x)^2)
K = 8.98755178787*10^9
e = 1.60217662*10^-19
R = 5.291772*10^-11
K*e^2 (1/(r - x)^2 + 1/(r + x)^2 - 2/r^2) - K*e^2 (1/(R - x)^2 - 1/(R + x)^2) = 0
K*e^2 [(1/(r - x)^2 + 1/(r + x)^2 - 2/r^2) - (1/(R - x)^2 - 1/(R + x)^2)] = 0
(1/(r - x)^2 + 1/(r + x)^2 - 2/r^2) - (1/(R - x)^2 - 1/(R + x)^2) = 0
(1/(10^-10-x)^2 + 1/(10^-10+x)^2 - (2/10^-18) - (1/(5.291772*10^-11-x)^2 - 1/(5.291772*10^-11+x)^2)= 0
Answer: Dipole offset distance above: X = 7.1789*10^-12 meter
(Check: External Coulomb force = 1.86963*10^-44 Newton)
(Internal Coulomb reaction force = 1.86962*10^-44 Newton)
Coulomb dipole gravity between the two atoms = 1.8696*10^-44 Newton
Calculation of Newton gravity between two hydrogen atoms 1*10^-10 meter apart.
F = G*(m1*m2)/r^2
F = 6.674*10^-11(1.67 x 10^-27)^2/(1*10^-10)^2
F = 1.86131*10^-44 Newton
Gravity between two hydrogen atoms according to Newton and the gravitational constant = 1.8613*10^-44 N.
Net Coulomb attraction between dipoles according to the above = 1.8696*10^-44 N.
The overwhelming correspondance of the two leaves no doubt about the fact that gravity is caused by the net Coulomb force between dipoles such as atoms.
Coulomb dipole gravity, dipole elongation and the atomic clock
An atomic clock runs 30 microseconds per day slower on earth than it does in GPS satellite orbit. This corresponds to a relative error of 3.472*10^-10.
A Hydrogen atomic clock uses hydrogen atoms as a frequency medium. In gravity free space a hydrogen atom is externally neutral while the electron orbit is centered around the proton. In earth gravity a hydrogen atom is slightly elongated into a dipole where the center of the electron orbit is offset from the center of charge of the proton. This slows the frequency of the electron orbit. Knowing the Coulomb attraction force between proton and electron in a hydrogen atom, as well as the Coulomb dipole gravity between the hydrogen atom and earth we can calculate the expected orbital disturbance and associated orbital frequency reduction of the electron in the hydrogen atom while in earth gravity.
1. Hydrogen atom centering force:
This is the electrostatic attraction between the electron and the proton in the hydrogen atom according to Coulombs law.
F1 = K(e*e)/r^2
K = 8.99×109 N m2 C^-2
e = 1.60217662 × 10^-19 Coulombs
r = Bohr's radius = 5.29×10^-11 m
F1 = 4.357*10^20 N
2. Dipole gravity distraction force:
This calculates the net dipole elongation force acting on the hydrogen atom.
F2 = K(n*e*e)/L^2
K = 8.99×109 N m2 C^-2
e = 1.60217662 × 10^-19 Coulombs
n = The dipole mass of earth divided by the dipole mass of one proton = (5.972*10^24) / (1.673*10^-27)
L = The distance between the hydrogen atom and the integrated center of effort of the dipole mass in earth, which is is at the center of the earth = the radius of the earth = 6378*10^3 m
F2 = 1.468*10^11 N
Assuming a linear relationship between relative dipole elongation force and relative hydrogen clock frequency, the error in clock frequency at the surface of the earth caused by Coulomb dipole gravity should be:
F2 / F1 = (1.468*10^11)/(4.357*10^20) = 3.369*10^-10
The atomic clock error to be expected at ground level, calculated using the effects of Coulomb polarization corresponds within 0.103*10^-10 to observed values. The difference in the last decimal is most likely the result of approximating the electron orbital as circular when in reality it is slightly elliptical.
Effective charge
A hydrogen atom unaffected by external influences is centered to where the center of the electron orbital coincides with the center of charge of the proton. The compound charge of this atom = 0. However, when in the proximity of other charges, including other atoms, an atom becomes polarized to where the center of the electron orbital does not coincide with the center of charge of the proton. A polarized atom acts as a dipole with a very low effective positive charge at one end and the corresponding negative charge at the other end.
Calculating the effective dipole charge (e) of two hydrogen dipoles under Coulomb electric gravity:
K*e^2/r^2 = G*m^2/r^2
K = 8.98755178787*10^9
G = 6.674*10^-11
m = 1.6737236*10^-27
e^2 = G*m^2/K = 6.674*10^-11*(1.6737236*10^-27)^2
e^2 = [6.674*10^-11*(1.6737236*10^-27)^2]/8.98755178787*10^9
e^2 = [6.674*10^-11*2.80127169*10^-54)]/8.98755178787*10^9
e^2 = 18.69567598*10^-65/8.98755178787*10^9
e^2 = 2.080*10^-74
e = 1.442*10^-37 Coulomb
Compare this to the charge of the proton (or electron):
1.60217662*10^-19 Coulomb
As can be seen from the above, the effective charge of a hydrogen atom dipole is in this case a minuscule portion of the charge of any of the two constituents, the proton and the electron:
1.442*10^-37 Coulomb / 1.60217662*10^-19 Coulomb = 9.000*10^-19 of the charge of a proton.
The effective charge and the subsequent force of gravity are consequently very weak compared to the charges and forces at work in for example strong force.
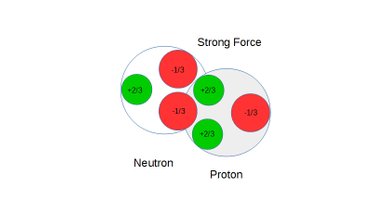
Deuterium binding energy
As a third method to quantify the expected consequences of Coulomb polarization, computer simulations were performed to map the locations of all charges including distances between charges and the directions of all dipole axis in deuterium. All attracting and repelling Coulomb binding forces were then calculated. The compound of these forces is the net binding force holding the proton and the neutron together in a deuterium atom. This compound net binding force, also known as strong force, is a short reach force which upon forced separation between the proton and the neutron goes to zero before turning into a repelling force. Integrating the compound binding force over the distance between maximum strong force and the attraction/repulsion cross over point yields the total binding energy of deuterium.
The binding energy of deuterium calculated as described and illustrated above corresponds within 1% to published values. For the full calculation of this binding energy contact the author below.
Neutrons and Protons
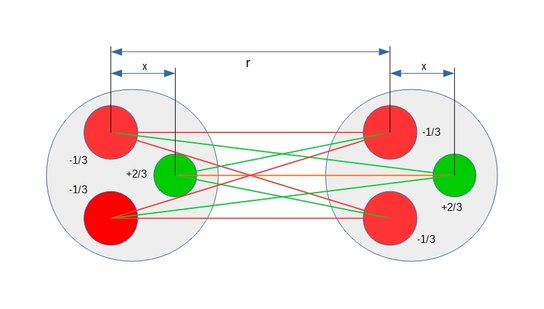
A mechanism similar to the dipole formation in interacting atoms has been observed in computer simulations involving quarks in interacting neutrons and protons. A neutron consists of one +2/3e up quark and two -1/3e down quarks giving the neutron an overall charge of zero.
Links to neutron gravity simulations:
Charge posturing and Coulomb attraction between 2 neutrons:
https://www.youtube.com/watch?v=fmsssEfkq1I
https://www.youtube.com/watch?v=bvdcgkuVLsY
Figure 3. Posturing between two neutrons:
Links to strong force simulations:
Quark posturing, Coulomb interactions and strong force between neutrons and protons:
https://www.youtube.com/watch?v=uLZ1OzCQ-Ws
https://www.youtube.com/watch?v=dCdnDJBEZuc
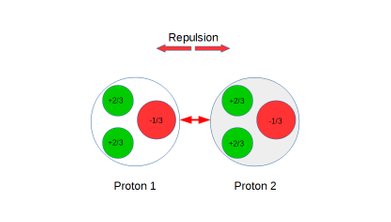
Quark posturing, Coulomb interactions and repulsion between protons:
https://www.youtube.com/watch?v=fZviCBkbnYw
https://www.youtube.com/watch?v=9XRmoAyMPvY
https://www.youtube.com/watch?v=EKrkHIBOjoQ
https://www.youtube.com/watch?v=JWhw7Jt5rIE
Quark posturing, Coulomb interaction and attraction prior to transmutation and strong force:
https://www.youtube.com/watch?v=BYHhevzyFJY
https://www.youtube.com/watch?v=iSVMdEs6bVc
Also see static figures below illustrating the concept of weak force repulsion, cross over point and strong force attraction:
Figure 5: Protons under repulsion.
Figure 6: Protons at the cross over point between repulsion and attraction.
Figure 7: Short reach strong coulomb force attraction
Figure 8: Neutron and proton under strong force
Dipole 1996-2023
Bengt E Nyman
Feel free to contact bengtenyman@yahoo.com